[Machine learning] 2. 지도 학습

본 포스팅은 “딥러닝 텐서플로 교과서” 책 내용을 기반으로 작성되었습니다. 잘못된 내용이 있을 경우 지적해 주시면 감사드리겠습니다.

2-1. 지도학습

지도 학습은 정답(=레이블)을 컴퓨터에 미리 알려주고 데이터를 학습시키는 방법이다. 지도 학습에는 크게 분류와 회귀가 있다. 분류는 주어진 데이터를 정해진 범주에 따라 분류하고, 회귀는 데이터들의 특성을 기준으로 연속된 값을 그래프로 표현하여 패턴이나 트렌드를 예측할 때 사용한다.

• 분류
  
  • 데이터 유형: 이산형 데이터
    
  • 결과: 훈련 데이터의 레이블 중 하나를 예측
    
• 회귀
  
  • 데이터 유형: 연속형 데이터
    
  • 결과: 연속된 값을 예측
    

2-2. K-최근접 이웃

• 왜 사용? → 주어진 데이터에 대한 분류
  
• 언제 사용? → 직관적이고 사용하기 쉬워 초보자가 쓰기 좋고, 훈련 데이터를 충분히 확보할 수 있는 환경에서 사용하면 좋음
  

K-최근접 이웃은 새로운 입력을 받았을 때 기존 클러스터에서 모든 데이터와 인스턴스(새로운 데이터 들어올 때 데이터와 데이터 사이의 거리를 측정한 관측치 의미) 기반 거리를 측정 후, 가장 많은 속성을 가진 클러스터에 할당하는 분류 알고리즘이다. K값을 어떻게 설정하느냐에 따라 새로운 데이터에 대한 분류 결과가 달라질 수 있다. iris 데이터를 활용한 코드 예제는 다음과 같다.

# 라이브러리 호출 및 데이터 준비
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import metrics

names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
dataset = pd.read_csv('iris.data', names=names)

# 훈련과 검증 데이터셋 분리
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 4].values

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

from sklearn.preprocessing import StandardScaler
s = StandardScaler()
s.fit(X_train)
X_train = s.transform(X_train)
X_test = s.transform(X_test)

# 모델 생성 및 훈련
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=50)
knn.fit(X_train, y_train)

# 모델 정확도
from sklearn.metrics import accuracy_score
y_pred = knn.predict(X_test)
print("정확도: {}".format(accuracy_score(y_test, y_pred)))

# 최적의 K 찾기
k=10
acc_array = np.zeros(k)
for k in np.arange(1, k+1, 1):
    classifier = KNeighborsClassifier(n_neighbors=k).fit(X_train, y_train)
    y_pred = classifier.predict(X_test)
    acc = accuracy_score(y_test, y_pred)
    acc_array[k-1] = acc

max_acc = np.amax(acc_array)
acc_list = list(acc_array)
k = acc_list.index(max_acc)
print("정확도", max_acc, "으로 최적의 k는", k+1, "입니다.")

(결과) 정확도: 0.8
       정확도 1.0 으로 최적의 k는 1 입니다.

K 값이 50일 때 정확도는 80%였는데, K 값이 1일 때 정확도는 100%로 높아졌다. 이처럼 K-최근접 이웃 알고리즘은 K 값에 따라 성능이 달라질 수 있으므로 초기 설정이 매우 중요하다.

2-3. 서포트 벡터 머신

• 왜 사용? → 주어진 데이터에 대한 분류
• 언제 사용? → 커널만 적절히 선택하면 정확도가 상당히 좋으므로 정확도를 요구하는 분류 문제를 다룰 때 사용하면 좋음. 또한 텍스트를 분류할 때도 많이 사용함.

서포트 벡터 머신(SVM)은 분류를 위한 기준선을 정의하는 모델이다. 분류되지 않은 새로운 데이터가 나타나면 결정 경계(기준선)를 기준으로 경계의 어느 쪽에 속하는지 분류하는 모델이다. 따라서 서포트 벡터 머신에서는 결정 경계를 이해하는 것이 중요하다.
결정 경계는 데이터를 분류하기 위한 기준선이다. 결정 경계는 데이터가 분류된 클래스에서 최대한 멀리 떨어져 있을 때 성능이 가장 좋다. 여기서 마진이라는 개념이 등장한다. 마진은 결정 경계와 서포트 벡터 사이의 거리를 의미한다. 서포트 벡터는 결정 경계와 가까이 있는 데이터들을 의미한다. 즉, 이 서포트 벡터들이 경계를 정의하는 결정적인 역할을 하게 된다. 최적의 결정 경계는 마진을 최대로 해야 한다.
서포트 벡터 머신은 데이터들을 올바르게 분리하면서 마진 크기를 최대화 해야한다. 여기서 이상치를 다루는 것이 가장 중요하다. 이상치를 허용하지 않는 것을 하드 마진이라 하며, 어느 정도의 이상치들이 마진 안에 포함되는 것을 허용하면 소프트 마진이라 한다.

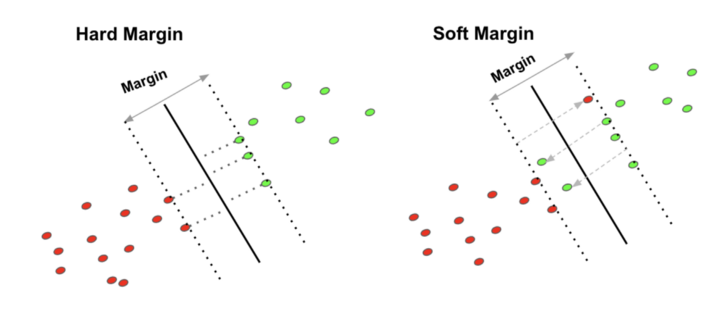
그림 2-1. 하드 마진과 소프트 마진

# 라이브러리 호출
from sklearn import svm
from sklearn import metrics
from sklearn import datasets
from sklearn import model_selection
import tensorflow as tf
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'

# iris 데이터를 준비하고 훈련과 검증 데이터 셋으로 분리
iris = datasets.load_iris()
X_train, X_test, y_train, y_test = model_selection.train_test_split(iris.data, iris.target, test_size=0.6, random_state=42)
svm = svm.SVC(kernel='linear', C=1.0, gamma=0.5) # ★
svm.fit(X_train, y_train)
predictions = svm.predict(X_test)
score= metrics.accuracy_score(y_test, predictions)
print('정확도: {0:f}'.format(score))

(결과) 정확도: 0.988889

주석으로 별표 처리 된 코드를 보자. SVM은 선형 분류와 비선형 분류를 지원한다. 비선형에 대한 커널은 선형으로 분류될 수 없는 데이터들 때문에 발생했다. 비선형 문제를 해결하는 가장 기본적인 방법은 저차원 데이터를 고차원으로 보내는 것이다. 하지만 이러한 작업은 많은 수학적 계산을 필요로 하여 선응에 문제를 줄 수 있다. 이러한 문제를 해결하고자 도입한 것이 ‘커널 트릭’이다. 선형 모델을 위한 커널에는 선형 커널이 있다. 비선형을 위한 커널에는 가우시안 RBF 커널과 다항식 커널이 있다.
가우시안 RBF 커널과 다항식 커널은 수학적 기교를 이용한 것으로, 벡터 내적을 계산한 후 고차원으로 보내는 방법으로 연산량을 줄였다.

• 선형 커널: 선형으로 분류 가능한 데이터에 적용
  $K(a,b)=a^{T}\cdot b$
  (a,b: 입력 벡터)
  
• 다항식 커널: 실제로는 특성을 추가하지 않았지만, 다항식 특성을 많이 추가한 것과 같은 결과를 얻을 수 있는 방법
  $K(a,b)=(\gamma a^{T}\cdot b)^{d}$
  (a,b: 입력 데이터, $\gamma$: 감마(gamma), d: 차원)
• 가우시안 RBF 커널: 다항식 커널의 확장. 입력 벡터를 차원이 무한한 고차원으로 매핑한 것으로 모든 차수의 모든 다항식 고려함
  $K(a,b)=exp(-\gamma \left | a-b \right |^{2})$
  ($\gamma$ 는 하이퍼파라미터)
  

C 값은 오류를 어느 정도 허용할지 지정하는 파라미터이다. C 값이 클수록 하드 마진, 작을 수록 소프트 마진이다.
감마는 결정 경계를 얼마나 유연하게 가져갈지 지정한다. 감마 값이 높으면 훈련 데이터에 많이 의존하여 결정 경계가 곡선 형태를 띠고 과적합을 초래할 수 있다.

2-4. 결정 트리

• 왜 사용? → 주어진 데이터에 대한 분류
• 언제 사용? → 이상치가 많은 값으로 구성된 데이터셋을 다룰 때 사용하면 좋음. 결정 과정이 시작적으로 표현되기 때문에 머신 러닝이 어떤 방식으로 의사 결정을 하는지 알고 싶을 때 유용.

결정 트리는 데이터를 분류하거나 결과값을 예측하는 분석 방법이다. 결과 모델이 트리 구조이므로 결정 트리라고 한다. 결정 트리는 데이터를 1차로 분류한 후 각 영역의 순도는 증가하고 불순도와 불확실성은 감소하는 방향으로 학습을 진행한다. 이를 정보이론에서는 정보 획득이라 하며 순도를 계산하는 방법에 따라 다음 두가지가 많이 사용된다.

1) 엔트로피
확률 변수의 불확실성을 수치로 나타낸 것으로 엔트로피가 높을수록 불확실성이 높다.

• 엔트로피 = 0 = 불확실성 최소 = 순도 최대
  
• 엔트로피 = 0.5 = 불확실성 최대 = 순도 최소
  $Entropy(A) = -\sum_{k=1}^{m}p_{k}log_{2}(p_{k})$
  $p_{k}$ : A 영역에 속하는 데이터 중 k 범주에 속하는 데이터 비율

2) 지니계수
불순도를 측정하는 지표로 데이터의 통계적 분산 정도를 정량화해서 표현한 값이다. 원소 n개 중 임의로 2개 추출할 때, 추출된 2개가 서로 다른 그룹에 속해 있을 확률을 의미한다.
$G(S) = 1-\sum_{i=1}^{c}p_{i}^{2}$ S: 이미 발생한 사건의 모음, c: 사건 개수

# 라이브러리 호출 및 데이터 준비
import pandas as pd
df = pd.read_csv('train.csv', index_col='PassengerId')
print(df.head)

# 데이터 전처리
df = df[['Pclass', 'Sex', 'Age', 'SibSp', 'Parch', 'Fare', 'Survived']]
df['Sex'] = df['Sex'].map({'male': 0, 'female': 1})
df = df.dropna()
X = df.drop('Survived', axis=1)
y = df['Survived']

# 훈련과 검증 데이터셋으로 분리
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)

# 결정 트리 모델 생성
from sklearn import tree
model = tree.DecisionTreeClassifier()

# 모델 훈련
model.fit(X_train, y_train)

# 모델 예측
y_predict = model.predict(X_test)
from sklearn.metrics import accuracy_score
accuracy_score(y_test, y_predict)

# 혼동 행렬을 이용한 성능 측정
from sklearn.metrics import confusion_matrix
pd.DataFrame(
    confusion_matrix(y_test, y_predict),
    columns=['Predicted Not Survival', 'Predicted Survival'],
    index=['True Not Survival', 'True Survival']
)

(결과) <bound method NDFrame.head of              Survived  Pclass  \
       PassengerId                     
       1                   0       3   
       2                   1       1   
       3                   1       3   
       4                   1       1   
       5                   0       3   
       ...               ...     ...   
       887                 0       2   
       888                 1       1   
       889                 0       3   
       890                 1       1   
       891                 0       3   
                                                               Name     Sex   Age  \
       PassengerId                                                                    
       1                                      Braund, Mr. Owen Harris    male  22.0   
       2            Cumings, Mrs. John Bradley (Florence Briggs Th...  female  38.0   
       3                                       Heikkinen, Miss. Laina  female  26.0   
       4                 Futrelle, Mrs. Jacques Heath (Lily May Peel)  female  35.0   
       5                                     Allen, Mr. William Henry    male  35.0   
       ...                                                        ...     ...   ...   
       887                                      Montvila, Rev. Juozas    male  27.0   
       888                               Graham, Miss. Margaret Edith  female  19.0   
       889                   Johnston, Miss. Catherine Helen "Carrie"  female   NaN   
       890                                      Behr, Mr. Karl Howell    male  26.0   
       891                                        Dooley, Mr. Patrick    male  32.0   
                   SibSp  Parch            Ticket     Fare Cabin Embarked  
       PassengerId                                                          
       1                1      0         A/5 21171   7.2500   NaN        S  
       2                1      0          PC 17599  71.2833   C85        C  
       3                0      0  STON/O2. 3101282   7.9250   NaN        S  
       4                1      0            113803  53.1000  C123        S  
       5                0      0            373450   8.0500   NaN        S  
       ...            ...    ...               ...      ...   ...      ...  
       887              0      0            211536  13.0000   NaN        S  
       888              0      0            112053  30.0000   B42        S  
       889              1      2        W./C. 6607  23.4500   NaN        S  
       890              0      0            111369  30.0000  C148        C  
       891              0      0            370376   7.7500   NaN        Q  
       [891 rows x 11 columns]>

그림 2-2. 코드 결과

2-5. 로지스틱 회귀

• 왜 사용? → 주어진 데이터에 대한 분류
• 언제 사용? → 주어진 데이터에 대한 확신이 없거나 추가적으로 훈련 데이터셋을 수집하여 모델을 훈련시킬 수 있느 환경에서 사용하면 유용

# 라이브러리 호출 및 데이터 준비
%matplotlib inline
from sklearn.datasets import load_digits
digits = load_digits()
print('Image Data Shape', digits.data.shape)
print("Label Data Shape", digits.target.shape)

(결과) Image Data Shape (1797, 64)
       Label Data Shape (1797,) ```python # digits 데이터셋의 시각화 import numpy as np import matplotlib.pyplot as plt plt.figure(figsize=(20, 4)) for index, (image, label) in enumerate(zip(digits.data[0:5], digits.target[0:5])):
plt.subplot(1, 5, index+1)
plt.imshow(np.reshape(image, (8, 8)), cmap=plt.cm.gray)
plt.title('Training: %i\n' % label, fontsize=20) ``` 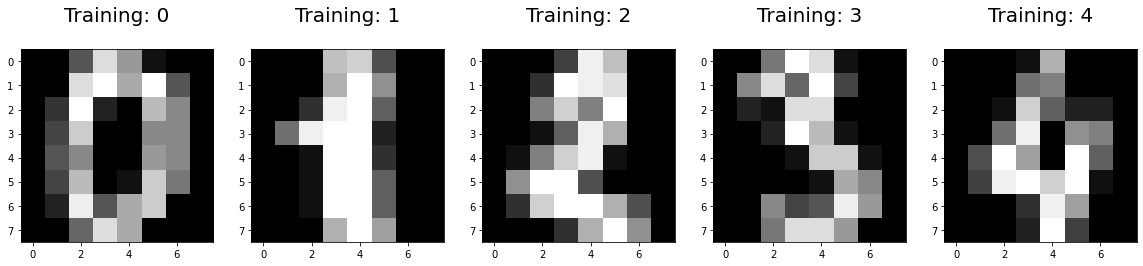![그림 2-3. 코드 결과](/assets/images/tensortextbook/2-3.png)

그림 2-3. 코드 결과

# 훈련과 검증 데이터셋 분리 및 로지스틱 회귀 모델 생성
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(digits.data, digits.target, test_size=0.25, random_state=0)
from sklearn.linear_model import LogisticRegression
logisticRegr = LogisticRegression()
logisticRegr.fit(x_train, y_train)

# 일부 데이터를 사용한 모델 예측
logisticRegr.predict(x_test[0].reshape(1, -1))
logisticRegr.predict(x_test[0:10])

# 전체 데이터를 사용한 모델 예측
predictions = logisticRegr.predict(x_test)
score = logisticRegr.score(x_test, y_test)
print(score)

(결과) 0.9511111111111111

# 혼동 행렬 시각화
import numpy as np
import seaborn as sns
from sklearn import metrics
cm = metrics.confusion_matrix(y_test, predictions)
plt.figure(figsize=(9, 9))
sns.heatmap(cm, annot=True, fmt=".3f", linewidth=.5, square=True, cmap='Blues_r')
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
all_sample_title = 'Accuracy Score: {0}'.format(score)
plt.title(all_sample_title, size=15)
plt.show()

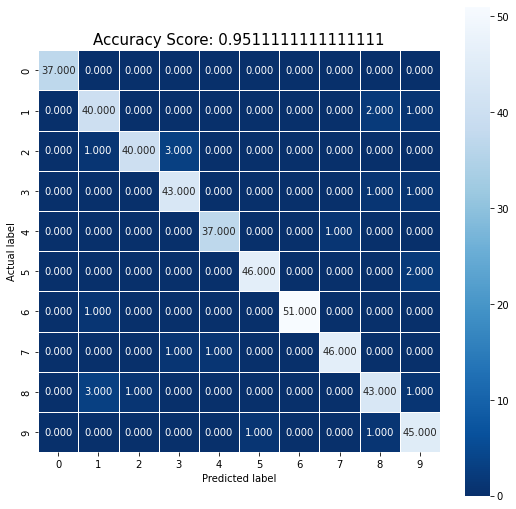
그림 2-4. 코드 결과

2-6. 선형 회귀

• 왜 사용? → 주어진 데이터에 대한 분류
• 언제 사용? 주어진 데이터에서 독립변수와 종속 변수가 선형관계 가질 때 사용하면 유용. 복잡한 연산 과정이 없어 컴퓨팅 성능이 낮은 환경이나 메모리 성능이 좋지 않을 때 사용하면 좋음.

# 라이브러리 호출
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as seabornInstance
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn import metrics
%matplotlib inline

# weather.csv 파일 불러오기
dataset = pd.read_csv('weather.csv')

# 데이터 간 관계를 시각화로 표현
dataset.plot(x='MinTemp', y='MaxTemp', style='o')
plt.title('MinTemp vs MaxTemp')
plt.xlabel('MinTemp')
plt.ylabel('MaxTemp')
plt.show()

그림 2-5. 코드 결과

# 데이터를 독립 변수와 종속 변수로 분리하고 선형 회귀 모델 생성
X = dataset['MinTemp'].values.reshape(-1, 1)
y = dataset['MaxTemp'].values.reshape(-1, 1)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
regressor = LinearRegression()
regressor.fit(X_train, y_train)

# 회귀 모델에 대한 예측
y_pred = regressor.predict(X_test)
df = pd.DataFrame({'Actual': y_test.flatten(), 'Predicted': y_pred.flatten()})
df

(결과) Actual	Predicted
       0	11.7	21.357510
       1	16.5	16.779398
       2	27.8	28.746743
       3	33.8	24.489902
       4	17.2	19.510201
       ...	...	...
       69	23.1	24.730855
       70	13.6	13.245417
       71	12.0	12.120968
       72	27.5	24.329266
       73	29.3	23.847360
       74 rows × 2 columns

# 검증 데이터셋을 사용한 회귀선 표현
plt.scatter(X_test, y_test, color='gray')
plt.plot(X_test, y_pred, color='red', linewidth=2)
plt.show()

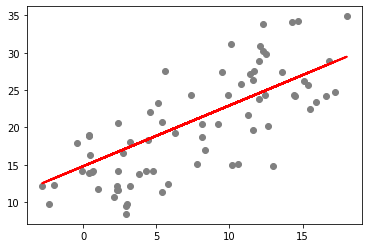
그림 2-6. 코드 결과

# 선형 회귀 모델 평가
print('평균제곱법:', metrics.mean_squared_error(y_test, y_pred))
print('루트 평균제곱법:', np.sqrt(metrics.mean_squared_error(y_test, y_pred)))

(결과) 평균제곱법: 21.93672902577098
       루트 평균제곱법: 4.683666194955719