[논문] 2. Deep One-Class Classification (Deep SVDD)
I. Motivation
- 해당 논문에서는 Deep Support Vector Data Description(Deep SVDD)를 소개한다. Deep SVDD는 초구(Hypersphere)의 부피를 최소화하는 신경망을 훈련함.
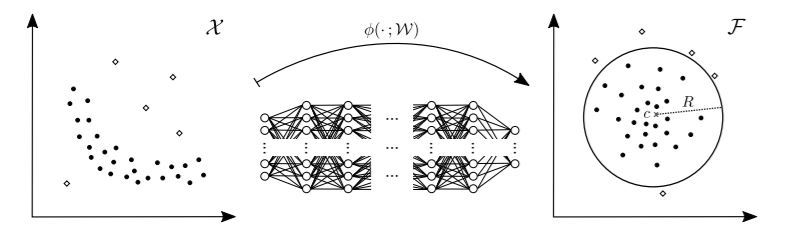
- 이 초구의 부피는 그림 2-1과 같이 데이터를 둘러싸서 정상 데이터의 범위를 나타내는 역할을 함.
- 초구의 부피를 최소화 하도록 훈련된 이 신경망은 데이터 포인트들을 초구의 중앙에 가깝게 매핑시켜 정상 데이터 내 공통 요인을 추출.
그림 2-1. Deep SVDD
II Deep SVDD
II.1 The Deep SVDD Objective
- Deep SVDD로 데이터를 둘러싼 가장 작은 사이즈를 갖는 초구를 찾기 위해 초구가 최소 부피를 갖도록 목적 함수를 빌드 하는 법에 대해 다룸.
- 수식
- Input 공간: $\chi \subseteq \mathbb{R}^{d}$
- Output 공간: $\xi \subseteq \mathbb{R}^{p}$
- 신경망: $\phi (\cdot ;\omega ) : \chi \rightarrow \xi$
- Weight 셋: $\omega = \{ \mathbf{W}^{1},…, \mathbf{W}^{L} \} $
- $\mathbf{W}^{l}$: 레이어 $l\in \{ 1,…,L \}$ 의 Weights
- $\phi (x ;\omega )\in \xi$: 파라미터 $\omega$ 를 갖는 신경망으로써 $\mathbf{x}\in \chi$ 의 feature를 표현
- Input 공간: $\chi \subseteq \mathbb{R}^{d}$
- Deep SVDD의 목적: 반지름 $R>0$ 을 갖고, 중앙 $c\in \xi$ 에 위치하며, 출력 공간 $\xi$ 에서 정상데이터를 잘 감싼, 초구가 최소의 부피를 갖도록 하는 매핑함수를 만들기 위해 최적의 파라미터 $\omega$ 을 학습하는것!
- $\chi$ 에서 훈련데이터 $D_{n}=\{ x_{1}, …, x_{n} \}$ 이 주어질 때, Soft-boundary Deep SVDD 목적함수는 그림 2-2와 같음.
그림 2-2. Soft-boundary Deep SVDD 목적함수
- 초구의 부피를 줄이려면, 위 식에서 $R^{2}$을 최소화 해야함.
- 그림 2-2에서 두번째 텀은 구 바깥에 놓인 점들에 대한 패널티 텀.
- 하이퍼파라미터 $v \in (0,1]$ 는 구의 부피(정상 범위)와 경계선 위반(이상치 범위) 사이의 트레이드오프를 조정.
-
마지막 텀은 신경망 파라미터 $\omega$ 에 대한 Weight 감쇠 규제이며, $ \lambda > 0 $ 이다. $ \| \cdot \|_F $ 는 프로베니우스 놈.
- 대부분의 훈련데이터가 정상이라 가정하면, 간단한 형태의 추가 목적함수(그림 2-3)를 활용할 수 있다.
그림 2-3. One-Class Deep SVDD 목적함수
- Soft-boundary Deep SVDD 목적함수와 One-Class Deep SVDD 목적함수 차이
- Soft-boundary Deep SVDD 목적함수는 초구 외부에 있는 데이터와 초구의 반지름에 패널티를 주어 초구를 축소시킴.
- One-Class Deep SVDD 목적함수는 모든 데이터와 초구 중앙의 평균 거리를 최소화 하여 초구를 축소시킴. 즉, 데이터들을 초구의 중앙 $\mathbf{c}$ 에 가깝게 매핑시키기 위해 신경망이 정상데이터의 공통 요소를 추출하도록 훈련되어야함.
- 테스트 포인트 $\mathbf{x}\in \chi $ 에 대해 Anomaly score $s$ 를 다음과 같이 정의함.
- $s(\mathbf{x})=\| \phi (\mathbf{x};\omega ^{*})-\mathbf{c} \|^{2}$
- $s(\mathbf{x})=\| \phi (\mathbf{x};\omega ^{*})-\mathbf{c} \|^{2}$
- $ \omega ^{*} $ 는 훈련된 모델의 신경망 파라미터.
- Soft-boundary Deep SVDD의 경우, 훈련 모델의 최종 반지름 $ R^{*} $ 을 빼서 socre를 조정함. 초구 안에 포인트가 위치하면 Negative score, 바깥에 위치하면 Positive score.
- Deep SVDD는 낮은 메모리 복잡도를 갖고, 이미 학습된 파라미터를 갖고 있으므로 빠른 테스팅이 가능.
II.2 Optimization of Deep SVDD
- 오차역전법을 활용하여 파라미터 $\omega$ 최적화하기 위해 확률적 경사 하강법(SGD) 사용함
- 여러개의 GPU 사용하여 각 배치 단위의 데이터들을 병렬로 처리할 수 있음
- 신경망 파라미터 $\omega$ 와 $R$ 은 스케일이 서로 다름
- 따라서, $R$ 은 고정시킨채 $\omega$ 에 대해서만 $k\in \mathbb{N}$ 에포크로 훈련시키고, $k$ 에포크 이후에는 업데이트 된 $\omega$ 을 갖는 신경망으로부터 반지름 $R$ 을 구함(Alternating minimization/block coordinate descent approach).

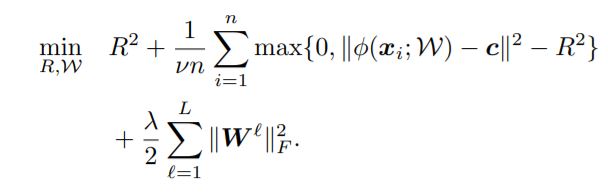
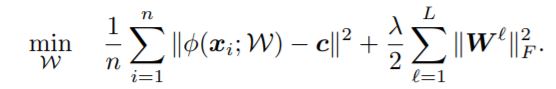
Leave a comment