[Deeplearning(Tensorflow)] 7. 순차 데이터와 순환 신경망

본 포스팅은 “혼자 공부하는 머신러닝+딥러닝” 책 내용을 기반으로 작성되었습니다. 잘못된 내용이 있을 경우 지적해 주시면 감사드리겠습니다.

7-1. 순차 데이터

순차 데이터(Sequential data)는 텍스트나 시계열 데이터(Time series data)와 같이 순서에 의미가 있는 데이터를 말한다. 텍스트 데이터는 단어의 순서가 중요한 순차 데이터이다. 이런 데이터는 순서를 유지하며 신경망에 주입해야 한다. 단어 순서를 마구 섞어서 주입하면 안된다. 이에 따라, 순차 데이터를 다룰 때는 이전에 입력한 데이터를 기억하는 기능이 필요하다.

완전 연결 신경망이나 합성곱 신경망은 정방향 계산을 수행하고 나면 그 샘플은 버려지고 다음 샘플을 처리할 때 재사용하지 않는다. 이처럼 입력 데이터의 흐름이 앞으로만 전달되는 신경망을 피드포워드 신경망(Feedforward neural network)라고 한다. 신경망이 이전에 처리했던 샘플을 다음 샘플을 처리하는데 재사용하려면 데이터 흐름이 앞으로만 전달되어서는 안된다. 다음 샘플을 위해 이전 데이터가 신경망 층에 순환될 필요가 있다.

7-2. 순환 신경망

순환 신경망(Recurrent neural network)은 뉴런의 출력이 다시 자기 자신으로 전달되는 신경망이다. A, B, C, 3개의 샘플을 처리하는 순환 신경망의 뉴런이 있다고 가정해보자. 첫 번째 샘플 A를 처리하고 난 출력 $O_{A}$ 가 다시 뉴런으로 들어간다. 이 출력에는 A에 대한 정보가 들어있다. 그 다음 B를 처리할 때 앞에서 A를 사용해 만든 출력 $O_{A}$ 를 함께 사용한다. $O_{A}$ 와 B를 사용해서 만든 $O_{B}$ 에는 A에 대한 정보가 어느 정도 포함되어 있다. 그 다음 C를 처리할 때 $O_{B}$ 를 함께 사용한다. $O_{B}$ 와 C를 사용해 만든 $O_{C}$ 에는 B에 대한 정보와 A에 대한 정보가 어느 정도 들어있다. 물론 A에 대한 정보보다는 B에 대한 정보가 더 많다. 그래서 순환 신경망에서는 ‘이전 샘플에 대한 기억을 가지고 있다’고 말한다. 이렇게 샘플을 처리하는 한 단계를 타임스텝(Timestep) 라고 한다.

순환 신경망은 이전 타임스텝의 샘플을 기억하지만, 타임스텝이 오래될수록 순환되는 정보는 희미해진다. 순환 신경망에서는 특별히 층을 셀(Cell)이라고 부른다. 한 셀에는 여러 개의 뉴런이 있지만 완전 연결 신경망과 달리 뉴런을 모두 표시하지 않고 하나의 셀로 층을 표현한다. 또 셀의 출력을 은닉 상태(Hidden state) 라고 부른다. 합성곱 신경망과 기본 구조는 비슷하다. 입력에 어떤 가중치를 곱하고 활성화 함수를 통과시켜 다음 층으로 보낸다. 달라지는 것은 층의 출력, 즉 은닉 상태를 다음 타입 스텝에 재사용하는 것이다.

일반적으로 은닉층의 활성화 함수로 하이퍼볼릭 탄젠트(Hyperbolic tangent) 함수인 tanh이 많이 사용된다. 이 함수는 -1~1 사이의 범위를 갖는다.

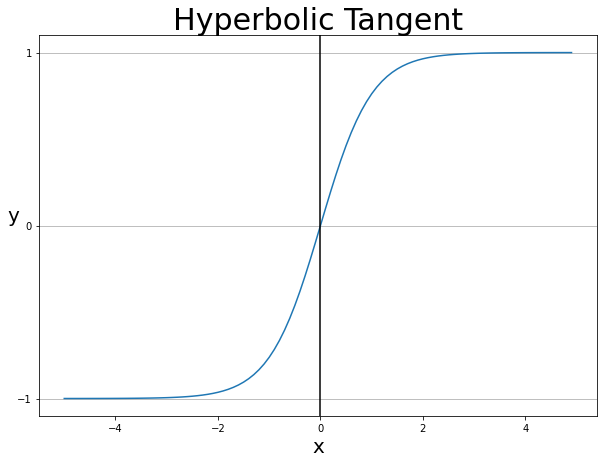
그림 7-1. 하이퍼볼릭 탄젠트

순환 신경망도 다른 신경망 처럼 입력과 가중치를 곱한다. 다만 가중치가 하나 더 있다. 바로 이전 타임스텝의 은닉 상태에 곱해지는 가중치이다. 셀은 입력과 이전 타임스텝의 은닉 상태를 사용하여 현재 타임스텝의 은닉 상태를 만든다. 즉, 입력에 곱해지는 가중치 $w_{x}$와 이전 타임스텝의 은닉 상태에 곱해지는 가중치 $w_{h}$가 있는 것이다. 또한 각 가중치에 절편도 하나씩 존재한다.

예를 들어보자. 타임스텝 1에서 셀의 출력 $h_{1}$이 타임스텝 2의 셀로 주입된다. 이 때 $w_{h}$와 곱해진다. 타임스텝 2에서 셀의 출력 $h_{2}$가 타임스텝 3의 셀로 주입된다. 이 때에도 $w_{h}$와 곱해진다. 여기에서 알 수 있는 것은 모든 타임스텝에서 사용되는 가중치는 $w_{h}$라는 것이다! 가중치 $w_{h}$는 타임스텝에 따라 변화되는 뉴런의 출력을 학습한다. 맨 처음 샘플을 입력할 때는 이전 타임스텝이 없다. 따라서 $h_{0}$은 모두 0으로 초기화 된다.

7-3. 셀의 가중치와 입출력

순환 신경망의 셀에서 필요한 가중치 크기를 계산해 보자. 특성의 개수가 4개이고 순환층의 뉴런이 3개라고 가정해보자. $w_{x}$는 4 x 3 = 12개이다. $w_{h}$는 어떨까? 첫 번째 뉴런 $r_{1}$의 은닉 상태가 다음 타임스텝에 재사용될 때, 첫 번째 뉴런과 두 번째 뉴런, 세 번째 뉴런에 모두 전달된다. 즉 이전 타임스텝의 은닉 상태는 다음 타음 스텝의 뉴런에 완전 연결된다! 두 번째 뉴런의 은닉 상태도 마찬가지로 첫 번째 뉴런과 두 번째 뉴런, 세 번째 뉴런에 모두 전달된다. 세 번째 뉴런도 동일하다. 이에 따라 $w_{h}$는 3 x 3 = 9개이다. 각 뉴런마다 하나의 절편이 있다. 따라서 이 순환층의 모델 파라미터 개수는 12 + 9 + 3 = 24개이다!

이번에는 순환층의 입력과 출력에 대해 보자. 합성곱 층은 너비, 높이, 채널 3개의 차원을 가졌다. 순환층은 일반적으로 샘플마다 2개의 차원을 갖는다. 보통 하나의 샘플을 하나의 시퀀스라고 말한다. 시퀀스 안에는 여러 개의 아이템이 있다. 시퀀스의 길이가 바로 타임스텝의 길이가 된다! 예를 들어 ‘I am a boy’란 문장이 있다고 하자. 이 샘플은 4개의 단어로 이루어져 있다. 각 단어를 3개의 어떤 숫자로 표현한다 해보자. 그럼 이 입력의 크기는 (1, 4, 3)이다. 이 입력이 순환층을 통과하면 두 번째, 세 번째 차원이 사라지고 순환층의 뉴런 개수만큼 출력된다.

다시 차근차근 보자. 하나의 샘플은 시퀀스 길이!(여기에서는 단어 개수!)와 단어 표현(여기서는 3개로 표현!)의 2차원 배열이다. 순환층을 통과하면 1차원 배열로 바뀐다. 1차원 배열의 크기는 순환층의 뉴런 개수에 의해 결정된다! 사실 순환층은 기본적으로 마지막 타임스텝의 은닉 상태만 출력으로 내보낸다. 이는 마치 입력된 시퀀스 길이를 모두 읽어서 정보를 마지막 은닉 상태에 압축하여 전달하는 것처럼 볼 수 있다.

순환 신경망도 다른 신경망처럼 여러 개의 층을 쌓을 수 있다. 이 때 셀의 입력은 샘플마다 타임스텝과 단어 표현으로 이루어진 2차원 배열이어야 한다. 따라서 이러한 상황에서는 첫 번째 셀이 마지막 타임스텝의 은닉 상태만 출력해서는 안된다. 이 경우에는 마지막 셀을 제외한 다른 모든 셀은 모든 타임스텝의 은닉 상태를 출력한다. 즉, 첫 번째 셀은 모든 타임스텝의 은닉 상태를 출력하고, 두 번째 셀은 마지막 타임스텝의 은닉 상태만 출력한다.

출력층은 다른 신경망처럼 순환 신경망도 마지막에 밀집층을 두어 클래스를 분류한다. 다중 분류일 경우 출력층에 클래스 개수만큼 뉴런을 두고 소프트맥스 활성화 함수를 사용한다. 이진 분류라면 하나의 뉴런을 두고 시그모이드 활성화 함수를 사용한다. 합성곱 신경망과 다른점은 마지막 셀의 출력이 1차원 이므로 Flatten 클래스를 둘 필요가 없다는 것이다.

마지막 예를 보자. 샘플이 20개의 타임스텝으로 이루어져 있고, 각 타임스텝은 100개의 표현 또는 특성으로 이루어져 있다 하자. 이 샘플이 순환층의 셀을 통과하면 모든 타임스텝을 처리하고 난 후 은닉 상태만 출력된다. 뉴런이 10개 있을 경우 이 은닉 상태의 크기는 (10,)가 된다. 이 샘플은 출력층에 바로 연결될 수 있다.