[Deeplearning(Tensorflow)] 6. 합성곱 신경망의 시각화

본 포스팅은 “혼자 공부하는 머신러닝+딥러닝” 책 내용을 기반으로 작성되었습니다. 잘못된 내용이 있을 경우 지적해 주시면 감사드리겠습니다.

6-1. 가중치 시각화

합성곱 층은 여러 개의 필터를 사용해 이미지에서 특징을 학습한다. 각 필터는 커널이라 부르는 가중치와 절편을 갖는다. 절편은 사실 시각적으로 의미가 있지는 않다. 가중치는 입력 이미지의 2차원 영역에 적용되어 어떤 특징을 크게 두드러지게 표현하는 역할을 한다.
만약 둥근 모서리를 뽑아내는 필터가 있다고 하자. 이 필터의 가중치는 둥근 모서리가 있는 영역에서 크게 활성화 되고, 그렇지 않은 영역에서는 낮은 값을 만든다. 즉, 곡선 부분의 가중치 값은 높고, 그 외 부분의 가중치 값은 낮을 것이다.
5장에서 만든 모델을 불러오자.

from tensorflow import keras
model = keras.models.load_model('best-cnn-model.h5')
model.layers

(결과) [<tensorflow.python.keras.layers.convolutional.Conv2D at 0x245e6418f28>,
       <tensorflow.python.keras.layers.pooling.MaxPooling2D at 0x245e6447860>,
       <tensorflow.python.keras.layers.convolutional.Conv2D at 0x245e6487ba8>,
       <tensorflow.python.keras.layers.pooling.MaxPooling2D at 0x245e66b23c8>,
       <tensorflow.python.keras.layers.core.Flatten at 0x245e66b26a0>,
       <tensorflow.python.keras.layers.core.Dense at 0x245e66bc320>,
       <tensorflow.python.keras.layers.core.Dropout at 0x245e66bc710>,
       <tensorflow.python.keras.layers.core.Dense at 0x245e66bce48>]

첫 번째 합성곱 층의 가중치를 보자. 층의 가중치와 절편은 weights 속성에 저장되어 있다.

conv = model.layers[0]
print(conv.weights[0].shape, conv.weights[1].shape)

(결과) (3, 3, 1, 32) (32,)

커널 크기가 3x3 이었고, 입력의 깊이는 1이었다. 출력 필터 개수가 32개 였으므로 올바르게 출력되었다는 것을 확인할 수 있다. 필터마다 1개의 절편이 있으므로 절편도 32개가 맞다. weights 속성은 다차원 배열인 Tensor 클래스의 객체이다. 다루기 쉽도록 numpy() 메소드로 넘파이 배열로 변환하고 가중치 배열의 평균과 표준편차를 구해보자.

conv_weights = conv.weights[0].numpy()
print(conv_weights.mean(), conv_weights.std())

(결과) -0.009519433 0.23307213

가중치의 평균이 0에 가깝고, 표준편차는 0.23 정도이다. 이 가중치가 어떤 분포를 가졌는지 확인해보자.

import matplotlib.pyplot as plt
plt.hist(conv_weights.reshape(-1, 1)) # (288, 1)
plt.xlabel('weight')
plt.ylabel('count')
plt,show()

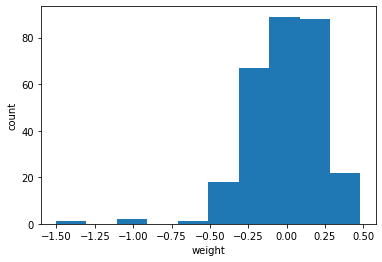
그림 6-1. 코드 결과

hist() 함수로 히스토그램을 그리려면 1차원 배열이 전달되어야 한다. 히스토그램을 보면 0을 중심으로 종 모양 분포를 띠고 있음을 볼 수 있다. 이 점을 일단 주목하자.
이번에는 32개의 커널을 출력해보자.

fig, axs = plt.subplots(2, 16, figsize=(15, 2))
for i in range(2):
    for j in range(16):
        axs[i, j].imshow(conv_weights[:, :, 0, i*16+j], vmin=-0.5, vmax=0.5)
        axs[i, j].axis('off')
plt.show()

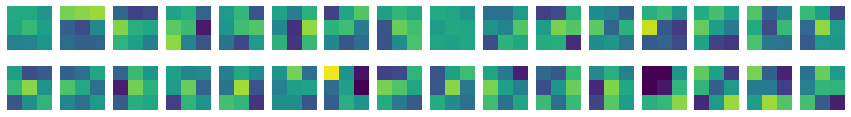
그림 6-2. 코드 결과

밝은 부분의 값이 가장 높다할 수 있다. 오른쪽 3픽셀 가중치 값이 가장 높은 커널이 있다고 하자. 이 가중치는 오른쪽에 놓인 직선을 만나면 크게 활성화 될 것이다. 참고로 imshow()의 vmin과 vmax는 절대값을 기준으로 픽셀의 강도를 나타내기 위해 사용했다. 즉 그 배열의 최대값이면 가장 밝은 노란색으로 그리는 것이다.
이제 훈련하지 않은 빈 합성곱 신경망을 만들고, 이 합성곱의 가중치가 위 코드에서 본 훈련된 가중치와 어떻게 다른지 보자.

no_training_model = keras.Sequential()
no_training_model.add(keras.layers.Conv2D(32, kernel_size=3, activation='relu', padding='same', input_shape=(28, 28, 1)))
no_training_conv = no_training_model.layers[0]
print(no_training_conv.weights[0].shape)

no_training_weights = no_training_conv.weights[0].numpy()
print(no_training_weights.mean(), no_training_weights.std())

plt.hist(no_training_weights.reshape(-1, 1))
plt.xlabel('weight')
plt.ylabel('count')
plt.show()

(결과) (3, 3, 1, 32)
       0.007826313 0.0833402

그림 6-3. 코드 결과

확실히 이전과 다르다. 대부분의 가중치가 -0.15~0.15 사이에 비교적 고르게 분포하고 있다. 이런 모양인 이유는 바로 텐서플로가 신경망의 가중치를 처음 초기화할 때 균등 분포에서 랜덤하게 값을 선택하기 때문이다.

fig, axs = plt.subplots(2, 16, figsize=(15, 2))
for i in range(2):
    for j in range(16):
        axs[i, j].imshow(no_training_weights[:, :, 0, i*16+j], vmin=-0.5, vmax=0.5)
        axs[i, j].axis('off')
plt.show()

그림 6-4. 코드 결과

전체적으로 필터의 가중치가 밋밋하게 초기화됐다. 이 그림을 훈련을 마친 가중치와 비교하면 합성곱 신경망이 패션 MIST 데이터셋의 분류 정확도를 높이기 위해 유용한 패턴을 학습했다는 것을 확인할 수 있다.

6-2. 함수형 API

만약 입력이 2개고 출력이 2개라면 지금까지 썼던 Sequential() 클래스를 사용하기 어렵다. 이 경우에는 함수형 API(Functional API)를 사용한다. 함수형 API는 케라스의 Model 클래스를 사용하여 모델을 만든다. 일단 Dense 층 2개를 만들어보자.

dense1 = keras.layers.Dense(100, activation='sigmoid')
dense2 = keras.layers.Dense(10, activation='softmax')

여기서 전에는 Sequential() 클래스의 add() 메소드에 위 객체들을 전달했다. 하지만 다음과 같이 함수처럼 호출도 가능하다.

hidden = dense1(inputs)
outputs = dense2(hidden)
model = keras.Model(inputs, outputs)

입력에서 출력까지 층을 호출한 결과를 계속 이어주고, Model 클래스에 입력과 최종 출력을 지정한다. 여기서 inputs은 어디서 왔을까? Sequential() 클래스는 InputLayer 클래스를 자동으로 추가하고 호출해 주었다. 하지만 Model() 클래스는 우리가 수동으로 InputLayer 클래스를 만들어 호출해야한다. 케라스는 InputLayer를 쉽게 다룰 수 있도록 Input() 함수를 별도로 제공한다.

inputs = keras.Inputs(shape=(784,))

참고로 케라스 모델은 layers 속성 외 InputLayer 객체를 포함한 _layers 속성을 따로 가지고 있다. Sequential 클래스 객체의 _layers 속성 첫 번째 항목이 바로 InputLayer 클래스의 객체이다. InputLayer 클래스는 모델의 입력을 첫 번째 은닉층에 전달하는 역할을 한다. 따라서 InputLayer 객체의 입력과 출력은 동일하다. 이제 전체를 합쳐보자!

inputs = keras.Input(shape=(784,))
hidden = dense1(inputs)
outputs = dense2(hidden)
model2 = keras.Model(inputs, outputs)

우리는 이제 특성 맵 시각화를 수행할 것이다. 그런데 이를 위해서는 함수형 API가 꼭 필요하다. 왜 일까?
우리는 6-1 장의 모델에서 첫 번째 Conv2D 출력이 필요하다. 만약 6-1 장의 model 객체 입력과 conv2D 출력을 알 수 있다면, 이 둘을 연결하여 새로운 모델을 얻을 수 있을 것이다. 우리는 첫 번째 Conv2D 층이 출력한 특성 맵을 원한다. 첫 번째 층의 출력은 Conv2D 객체의 output 속성에서 얻을 수 있다. model.layers[0].output 처럼 참조가 가능하다. model 객체의 입력은 input 속성으로 입력을 참조할 수 있다.

print(model.input)
conv_acti = keras.Model(model.input, model.layers[0].output)

(결과) Tensor("conv2d_4_input_2:0", shape=(None, 28, 28, 1), dtype=float32)

6-3. 특성 맵 시각화

패션 MNIST 데이터셋의 훈련 세트에 있는 첫 번째 샘플을 그려보자.

(train_input, train_target), (test_input, test_target) = keras.datasets.fashion_mnist.load_data()
plt.imshow(train_input[0], cmap='gray_r')
plt.show()

그림 6-5. 코드 결과

앵클 부츠다. 이 샘플을 conv_acti 모델에 넣어 Conv2D 층이 만드는 특성 맵을 출력해보자. predict() 메소드는 항상 입력의 첫 번째 차원이 배치 차원이다. 이를 위해 슬라이싱 연산자로 첫 번째 샘플을 선택하고 정규화하여 conv_acti 모델의 출력을 확인해보자.

inputs = train_input[0:1].reshape(-1, 28, 28, 1) / 255.0
feature_maps = conv_acti.predict(inputs)
print(feature_maps.shape)

(결과) (1, 28, 28, 32)

세임 패딩과 32개 필터를 사용하였으므로 올바른 출력 크기가 나왔다. 이제 32개의 특성맵을 그려보자.

fig, axs = plt.subplots(4, 8, figsize=(15, 8))
for i in range(4):
    for j in range(8):
        axs[i, j].imshow(feature_maps[0,:,:,i*8+j])
        axs[i, j].axis('off')
plt.show()

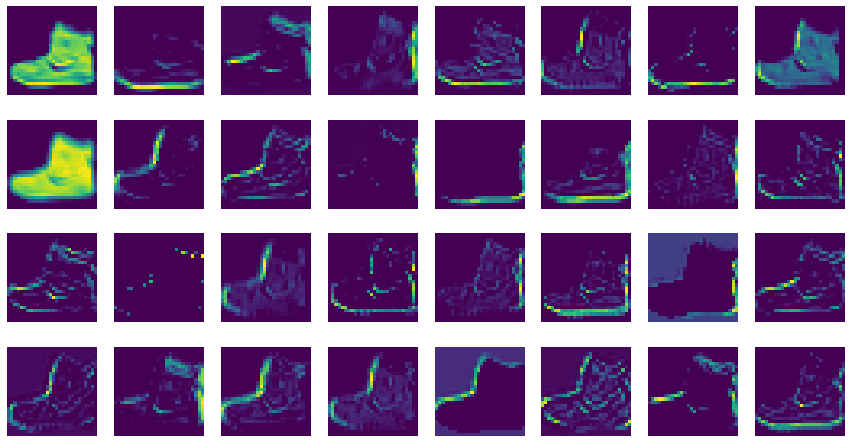
그림 6-6. 코드 결과

이 특성 맵은 32개의 필터로 인해 입력 이미지에서 강하게 활성화된 부분을 보여준다. 첫 번째 필터는 전체적으로 밝은색이고 전면이 모두 칠해진 영역을 감지한다. 흑백 부츠 이미지에서 검은 영역이 모두 잘 활성화 되었다.
두 번째 합성곱 층이 만든 특성 맵도 같은 방식으로 확인 가능하다. conv2_acti 모델고 마찬가지로 출력을 확인하자.

conv2_acti = keras.Model(model.input, model.layers[2].output)
inputs = train_input[0:1].reshape(-1, 28, 28, 1) / 255.0
feature_maps = conv2_acti.predict(inputs)
print(features_maps.shape)

(결과) (1, 14, 14, 64)

첫 번째 풀링 층에서 가로세로 크기가 반으로 줄었다. 필터 개수는 64개 이므로 출력 크기는 맞다. 이제 특성 맵을 시각화 해보자.

fig, axs = plt.subplots(8, 8, figsize=(12, 12))
for i in range(8):
    for j in range(8):
        axs[i, j].imshow(feature_maps[0,:,:,i*8+j])
        axs[i, j].axis('off')
plt.show()

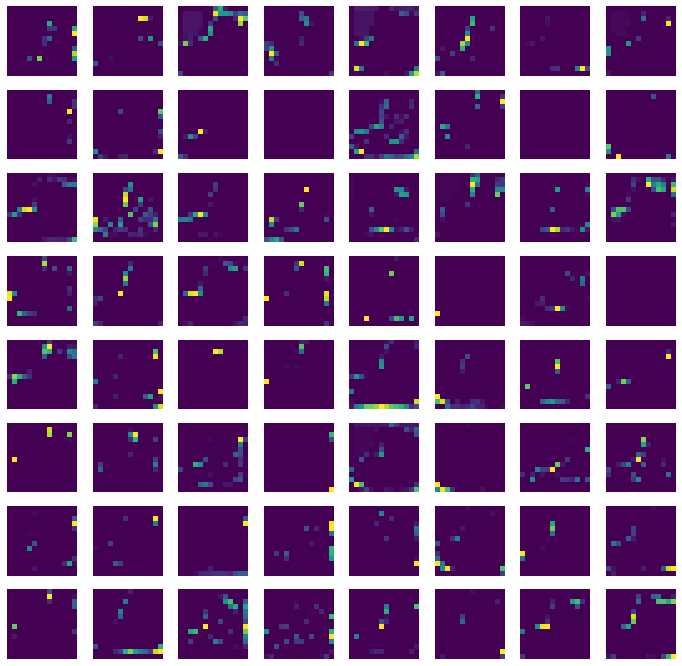
그림 6-7. 코드 결과

두 번째 합성곱 층의 필터 크기는 (3, 3, 32) 이다. 풀링 층에서 나온 (14, 14, 32) 특성 맵의 어떤 부위를 감지하는지 직관적으로 이해하기 어렵다. 합성곱 층을 많이 쌓을 수록 이러한 현상은 심해진다. 합성곱 신경망의 앞부분에 있는 합성곱 층은 이미지의 시각적인 정보를 감지한다. 반면 뒤쪽에 있는 합성곱 층은 앞쪽에서 감지한 시각적인 정보를 바탕으로 추상적인 정보를 학습한다고 볼 수 있다. 그렇기 때문이 합성곱 신경망이 패션 MNIST 이미지를 인식하여 10개의 클래스를 찾아낼 수 있는 것이다!