[Deeplearning(Tensorflow)] 2. 심층 신경망

본 포스팅은 “혼자 공부하는 머신러닝+딥러닝” 책 내용을 기반으로 작성되었습니다. 잘못된 내용이 있을 경우 지적해 주시면 감사드리겠습니다.

2-1. 2개의 층

from tensorflow import keras
(train_input, train_target), (test_input, test_target) = keras.datasets.fashion_mnist.load_data()

from sklearn.model_selection import train_test_split
train_scaled = train_input / 255.0
train_scaled = train_scaled.reshape(-1, 28*28)
train_scaled, val_scaled, train_target, val_target = train_test_split(train_scaled, train_target, test_size=0.2, random_state=42)

1장과 약간 다르게 입력층과 출력층 사이에 밀집층을 추가해볼 것이다. 입력층과 출력층 사이에 있는 모든 층을 은닉충(Hidden layer) 라고 한다. 은닉층에도 활성화 함수가 존재한다. 활성화 함수는 신경망 층의 선형 방정식의 계산 값에 적용하는 함수이다. 출력층에서는 이진 분류일 경우 시그모이드 함수, 다중 분류일 경우 소프트맥스 함수로 활성화 함수가 제한되었다. 그러나 은닉층의 활성화 함수는 비교적 자유롭다. 참고로 회귀의 출력은 임의의 어떤 숫자이므로 활성화 함수를 적용하지 않아도 된다.
우리는 왜 은칙층에 활성화 함수를 적용해야 할까? 만약 활성화 함수 없이 선형적인 산술 계산만 은닉층에서 수행한다면, 사실 은닉층이 수행하는 역할은 없는거나 마찬가지다. 선형 계산을 적당하게 비선형으로 비틀어 주어야 나름의 은닉층 역할을 수행할 수 있게 된다.

dense1 = keras.layers.Dense(100, activation='sigmoid', input_shape=(784, ))
dense2 = keras.layers.Dense(10, activation='softmax')

은닉층의 뉴런 개수를 정하는데 특별한 기준은 없다. 몇 개의 뉴런을 두어야 할지 판단하려면 상당한 경험이 필요하다. 그렇지만 한가지 제약사항은 있다. 적어도 출력층의 뉴런보다는 많게 만들어야 한다. 예를 들어, 클래스 10개에 대한 확률을 예측하는데, 이전 은닉층의 뉴런이 10개보다 적다면 부족한 정보가 전달될 것이다.

2-2. 심층 신경망 만들기

이제 앞에서 만든 dense1과 dense2 객체를 Sequential 클래스에 추가하여 심층 신경망(Deep neural network)을 만들어보자.

model = keras.Sequential([dense1, dense2])

출력층은 꼭 가장 마지막에 두어야 한다!
케라스 모델의 summary() 메소드를 호출하여 층에 대한 유용한 정보를 얻어보자.

model.summary()

(결과) Model: "sequential"
       _________________________________________________________________
       Layer (type)                 Output Shape              Param #   
       =================================================================
       dense_2 (Dense)              (None, 100)               78500     
       _________________________________________________________________
       dense_3 (Dense)              (None, 10)                1010      
       =================================================================
       Total params: 79,510
       Trainable params: 79,510
       Non-trainable params: 0
       _________________________________________________________________

출력을 보면 첫 줄에는 모델 이름이 나온다. 그 다음 모델에 들어 있는 층이 순서대로 나열된다. 층마다 층 이름, 클래스, 출력 크기, 모델 파라미터 개수가 나온다. 층을 만들 때 name 매개변수로 이름을 지정할 수 있다. 출력 크기를 보면 샘플개수가 정의되어 있지 않아 None으로 나온다. 왜 그럴까? 바로 사용자가 batch_size 매개변수로 미니 배치 개수를 지정할 수 있기 때문이다. 따라서 샘플 개수를 고정하지 않고 어떤 배치 크기에도 유연하게 대응할 수 있도록 None으로 설정한다. 이렇게 신경망 층에 입력되거나 출력되는 배열의 첫 번째 차원을 배치 차원 이라고 부른다.
모델 파라미터 개수를 보면 처음에 78,500개가 존재한다. 입력층 784개의 뉴런에 은닉층의 100개 뉴런을 곱하면 78,400개가 된다. 여기에 은닉층 100개 뉴런의 절편 개수까지 더하면 78,500개가 된다. 두번째 파라미터 개수는 100 x 10 + 10 으로 1,010개가 된다! 총 모델 파라미터 개수와 훈련되는 파라미터 개수가 동일하게 79,510개로 나온다. Non-trainable params는 0으로 나오는데, 간혹 경사 하강법으로 훈련되지 않는 파라미터를 가진 층이 있다. 이런 층이 여기에 나타나게 된다.

2-3. 층을 추가하는 다른 방법

첫번째 방법.

model = keras.Sequential([
    keras.layers.Dense(100, activation='sigmoid', input_shape=(784,), name='hidden'),
    keras.layers.Dense(10, activation='softmax', name='output')
], name = '패션 MNIST 모델')

model.summary()

(결과) Model: "패션 MNIST 모델"
       _________________________________________________________________
       Layer (type)                 Output Shape              Param #   
       =================================================================
       hidden (Dense)               (None, 100)               78500     
       _________________________________________________________________
       output (Dense)               (None, 10)                1010      
       =================================================================
       Total params: 79,510
       Trainable params: 79,510
       Non-trainable params: 0
       _________________________________________________________________

두번째 방법.

model = keras.Sequential()
model.add(keras.layers.Dense(100, activation='sigmoid', input_shape=(784,)))
model.add(keras.layers.Dense(10, activation='softmax'))

model.summary()

(결과) Model: "sequential_1"
       _________________________________________________________________
       Layer (type)                 Output Shape              Param #   
       =================================================================
       dense_4 (Dense)              (None, 100)               78500     
       _________________________________________________________________
       dense_5 (Dense)              (None, 10)                1010      
       =================================================================
       Total params: 79,510
       Trainable params: 79,510
       Non-trainable params: 0
       _________________________________________________________________

이제 모델을 훈련해보자. compile() 메소드 설정은 1장과 동일하다.

model.compile(loss='sparse_categorical_crossentropy', metrics='accuracy')
model.fit(train_scaled, train_target, epochs=5)

(결과) Epoch 1/5
       1500/1500 [==============================] - 4s 3ms/step - loss: 0.5649 - accuracy: 0.8062
       Epoch 2/5
       1500/1500 [==============================] - 3s 2ms/step - loss: 0.4097 - accuracy: 0.8527
       Epoch 3/5
       1500/1500 [==============================] - 3s 2ms/step - loss: 0.3735 - accuracy: 0.8643
       Epoch 4/5
       1500/1500 [==============================] - 4s 2ms/step - loss: 0.3517 - accuracy: 0.8726
       Epoch 5/5
       1500/1500 [==============================] - 3s 2ms/step - loss: 0.3342 - accuracy: 0.8786
       <tensorflow.python.keras.callbacks.History at 0x18340fc20f0>

몇 개의 층을 추가해도 compile() 메소드와 fit() 메소드 사용법은 동일하다.

2-4. 렐루 함수

시그모이드 함수의 식은 다음과 같다.
$\phi = \frac{1}{1+e^{-x}}$
이를 그래프로 나타내면 다음과 같다.

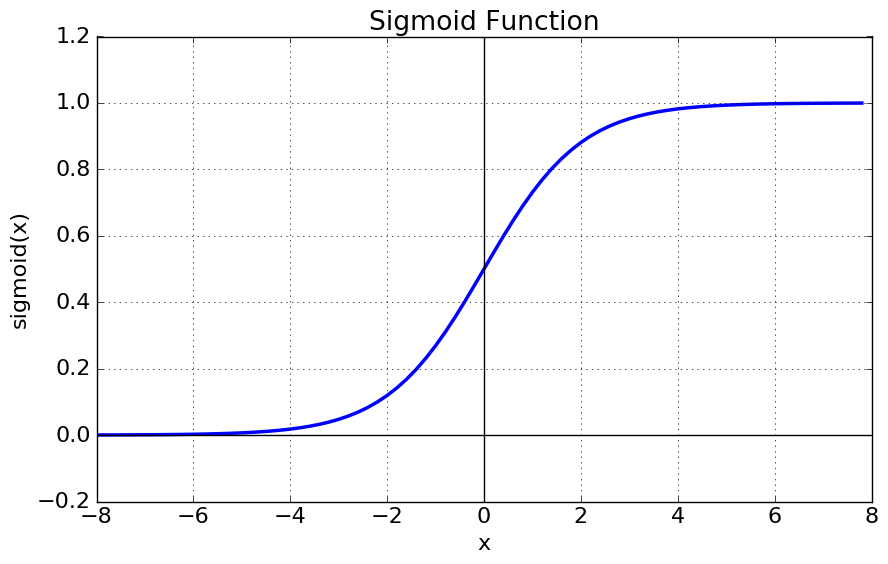
그림 2-1. 시그모이드 함수

보다시피 오른쪽과 왼쪽 끝으로 갈수록 그래프가 누워있다. 그러므로 올바른 출력을 만드는데 신속한 대응이 어렵다. 특히 층이 많은 심층 신경망에서는 그 효과가 누적되어 학습을 더 어렵게 만든다.
렐루(ReLU) 함수는 이러한 문제를 해결해준다. 입력이 양수일 경우 마치 활성화 함수가 없는 것처럼 그냥 입력을 통과시키고 음수일 경우 0으로 만든다.

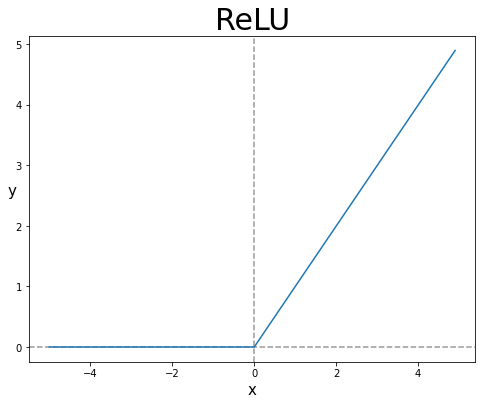
그림 2-2. 렐루 함수

렐루 함수는 max(0,z)로 표현할 수 있다. z가 0보다 크면 z를 출력하고 0보다 작으면 0을 출력한다. 렐루 함수는 이미지 처리에서 특히 좋은 성능을 낸다고 알려져 있다.

지금까지 1차원 형태로 이미지를 변형할 때 우리는 reshape() 메소드를 활용했다. 케라스에서는 Flatten 층을 제공해준다. Flatten 클래스는 배치 차원을 제외하고 나머지 입력 차원을 모두 일렬로 펼치는 역할만 한다. 입력에 곱해지는 가중치나 절편은 전혀 없다. 입력층 바로 뒤에 Flatten 층을 추가해보자.

model = keras.Sequential()
model.add(keras.layers.Flatten(input_shape=(28, 28))
model.add(keras.layers.Dense(100, activation='relu'))
model.add(keras.layers.Dense(10, activation='softmax'))
model.summary()

(결과) Model: "sequential_2"
       _________________________________________________________________
       Layer (type)                 Output Shape              Param #   
       =================================================================
       flatten (Flatten)            (None, 784)               0         
       _________________________________________________________________
       dense_6 (Dense)              (None, 100)               78500     
       _________________________________________________________________
       dense_7 (Dense)              (None, 10)                1010      
       =================================================================
       Total params: 79,510
       Trainable params: 79,510
       Non-trainable params: 0
       _________________________________________________________________

Flatten 층이 학습하는 층이 아니므로 모델 파라미터는 0개이다.
이제 해당 모델로 훈련 시켜보자.

(train_input, train_target), (test_input, teset_target) = keras.datasets.fashion_mnist.load_data()
train_scaled = train_input / 255.0
train_scaled, val_scaled, train_target, val_target = train_test_split(train_scaled, train_target, test_size=0.2, random_state=42)

model.compile(loss='sparse_categorical_crossentropy', metrics='accuracy')
model.fit(train_scaled, train_target, epochs=5)

(결과) Epoch 1/5
       1500/1500 [==============================] - 3s 2ms/step - loss: 0.5275 - accuracy: 0.8127
       Epoch 2/5
       1500/1500 [==============================] - 3s 2ms/step - loss: 0.3914 - accuracy: 0.8594: 0s - loss:
       Epoch 3/5
       1500/1500 [==============================] - 3s 2ms/step - loss: 0.3521 - accuracy: 0.8724
       Epoch 4/5
       1500/1500 [==============================] - 3s 2ms/step - loss: 0.3327 - accuracy: 0.8812: 0s - loss: 0.3317 - accuracy: 
       Epoch 5/5
       1500/1500 [==============================] - 3s 2ms/step - loss: 0.3160 - accuracy: 0.8865
       <tensorflow.python.keras.callbacks.History at 0x18340930898>

model.evaluate(val_scaled, val_target)

(결과) 375/375 [==============================] - 1s 2ms/step - loss: 0.3614 - accuracy: 0.8764
       [0.3613932430744171, 0.8764166831970215]

시그모이드 함수를 사용했을 때보다 성능이 조금 더 향상됐다.

2-5. 옵티마이저

케라스는 기본적으로 미니배치 경사 하강법을 사용하며 미니배치 개수는 32개이다. fit() 메소드의 batch_size 매개변수에서 이를 조정할 수 있다. compile() 메소드에서 우리는 loss와 metric 매개변수를 건들었다. 그러나 이 외에도 케라스는 다양한 종류의 경사 하강법 알고리즘을 compile() 메소드를 통해 제공한다. 이들을 옵티마이저(Optimizer) 라고 부른다.
가장 기본적인 옵티마이저는 SGD 이다.

model.compile(optimizer='SGD', loss='sparse_categorical_crossentropy', metrics='accuracy')

위 코드는 다음 코드와 완전히 동일하다.

sgd = keras.optimizer.SGD()
model.compile(optimizer=sgd, loss='sparse_categorical_crossentropy', metrics='accuracy')

만약 SGD의 학습률을 바꾸고 싶다면 다음과 같이 learning_rate 매개변수에서 지정하자.

sgd = keras.optimizer.SGD(learning_rate=0.1)

SGD외에도 여러 옵티마이저들이 있다. SGD 클래스의 momentum 매개변수는 기본값이 0이다. 0보다 큰 값으로 지정하면 마치 이전의 그레이디언트를 가속도처럼 사용하는 모멘텀 최적화(Momentum optimization)를 사용하게 된다. 보통 0.9이상의 값을 주어 사용한다. SGD 클래스의 nesterov 매개변수를 기본값 False에서 True로 바꾸면 네스테로프 모멘텀 최적화(Nesterov momentum optimization)을 사용한다.

sgd = keras.optimization.SGD(momentum=0.9, nesterov=True)

네스테로프 모멘텀은 최적화를 2번 반복하여 구현한다. 보통 네스테로프 모멘텀 최적화가 기본 SGD보다 더 나은 성능을 보여준다.
모델이 최적점에 가까이 갈수록 학습률을 낮출 수 있다. 안정적으로 최적점 수렴에 도달할 가능성이 높다. 이런 학습률을 적응적 학습률(Adaptive learning rate)라고 한다. 학습률 매개변수를 튜닝하는 수고를 덜 수 있다는게 장점이다. 대표적인 옵티마이저로는 Adagrad와 RMSprop이 있다. 기본값은 RMSprop이다.

adagrad = keras.optimizers.Adagrad()
model.compile(optimizer=adagrad, loss='sparse_categorical_crossentropy', metrics='accuracy')
rmsprop = keras.optimizers.RMSprop()
model.compile(optimizer=rmsprop, loss='sparse_categorical_crossentropy', metrics='accuracy')

참고로 모멘텀 최적화와 RMSProp 장점을 접목한 것이 Adam이다. 케라스는 Adam 클래스도 제공하며 learning_rate 매개변수의 기본값은 모두 0.001이다. adam으로 모델을 훈련시켜보자.

model = keras.Sequential()
model.add(keras.layers.Flatten(input_shape=(28, 28)))
model.add(keras.layers.Dense(100, activation='relu'))
model.add(keras.layers.Dense(10, activation='softmax'))
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics='accuracy')
model.fit(train_scaled, train_target, epochs=5)

(결과) Epoch 1/5
       1500/1500 [==============================] - 3s 2ms/step - loss: 0.5268 - accuracy: 0.8141
       Epoch 2/5
       1500/1500 [==============================] - 3s 2ms/step - loss: 0.3917 - accuracy: 0.8584
       Epoch 3/5
       1500/1500 [==============================] - 3s 2ms/step - loss: 0.3528 - accuracy: 0.8712
       Epoch 4/5
       1500/1500 [==============================] - 3s 2ms/step - loss: 0.3269 - accuracy: 0.8799
       Epoch 5/5
       1500/1500 [==============================] - 3s 2ms/step - loss: 0.3092 - accuracy: 0.8868
       <tensorflow.python.keras.callbacks.History at 0x18340a10e10>

model.evaluate(val_scaled, val_target)

(결과) 375/375 [==============================] - 1s 2ms/step - loss: 0.3467 - accuracy: 0.8719
       [0.3467445373535156, 0.871916651725769]