[Deeplearning(pytorch)] 3. 신경망 모델 구현하기

본 포스팅은 “펭귄브로의 3분 딥러닝, 파이토치맛” 책 내용을 기반으로 작성되었습니다. 잘못된 내용이 있을 경우 지적해 주시면 감사드리겠습니다.

3-1. 인공 신겸망(ANN)

인공 신경망(Artificial Neural Network)는 인간의 뇌 혹은 신경계의 작동 방식에서 영감을 받았다.

• 입력층: 인공 신경망에서 자극을 입력받는 감각기관에 해당하는 부분
• 은닉층: 입력층을 거친 자극을 처리해 다음 은닉층(인접한 신경세포)로 전달하는 부분. 이렇게 여러 은닉층을 거쳐 자극이 처리되다 보면, 자극에 따라 다양한 반응을 보이게 됨.
• 출력층: 은닉층을 거쳐 처리된 자극이 거치는 마지막 뉴런.
• 노드: 각 층에 존재하는 한 단위의 인공뉴런

하나의 생물학적 신경세포는 인접한 신경세포로 자극을 전달하기 전, 입력받은 자극에 여러 화학적 처리를 가함. 이와 비슷하게 인공 신경망도 가중치와 편향을 이용하여 데이터를 처리한다.

• 가중치: 입력 신호가 출력에 주는 영향을 계산하는 매개변수
• 편향: 노드가 얼마나 데이터에 민감한지 알려주는 매개변수
• 활성화 함수: 입력에 적절한 처리를 하여 출력 신호로 변환하는 함수. 입력 신호의 합이 활성화를 일으키는지 아닌지를 정의. 즉 다음 뉴런으로 자극(데이터)을 어느정도 활성화시켜 전달할지를 알려줌!

각 층마다 가중치 곱과 활성화 함수를 거치고, 이렇게 층 간 자극 처리와 전달 과정을 몇 겹 걸쳐 반복한 후 마지막 출력층에서 결과값을 만들어내는 것이 인공 신경망의 기본적인 작동 원리이다.
그 다음, 인공 신경망의 출력층이 낸 결과값과 정답을 비교하여 오차를 계산한다. 이 오차를 기반으로 경사하강법을 활용해 출력층의 가중치부터 입력층의 가중치까지 모두 변경해준다. 이렇게 전체 층의 가중치를 뒤에서부터 차례대로 조정하고 최적화하는 알고리즘이 바로 역전파 알고리즘이다.

3-2. 간단한 분류 모델 구현하기

지도학습 중 분류를 하는 간단한 ANN을 만들어보자. 넘파이, 사이킷런, 맷플롯립을 임포트 할 것이다.

• 넘파이: 유명한 수치해석용 라이브러리. 행렬과 벡터 연산에 유용. 파이토치도 이 넘파이를 활용하여 개발됨.
• 사이킷런: 파이썬의 대표적인 머신러닝 라이브러리. 딥러닝을 제외한 머신러닝은 거의 이 라이브러리 쓴다 봐도 무방.

import torch
import numpy
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import torch.nn.functional as F

먼저 신경망 학습과 평가에 사용할 데이터셋을 만든다.

n_dim = 2
# 2차원 벡터 형태로 4개의 클러스터 갖는 데이터 만듬. 각 데이터는 0, 1, 2, 3으로 인덱싱 됨.
x_train, y_train = make_blobs(n_samples=80, n_features=n_dim, centers=[[1,1], [-1,-1], [1,-1], [-1,1]], shuffle=True, cluster_std=0.3)
x_test, y_test = make_blobs(n_samples=20, n_features=n_dim, centers=[[1,1], [-1,-1], [1,-1], [-1,1]], shuffle=True, cluster_std=0.3)

# 0번과 1번 레이블 갖는 데이터는 전부 0번, 2번과 3번 레이블 갖는 데이터는 전부 1번
def label_map(y_, from_, to_):
  y = numpy.copy(y_)
  for f in from_:
    y[y_ == f] = to_
  return y

y_train = label_map(y_train, [0, 1], 0)
y_train = label_map(y_train, [2, 3], 1)
y_test = label_map(y_test, [0, 1], 0)
y_test = label_map(y_test, [2, 3], 1)

데이터가 잘 만들어졌는지 시각화 해보자.

def vis_data(x, y = None, c = 'r'):
  if y is None:
    y = [None] * len(x)
  for x_, y_ in zip(x, y):
    if y_ is None:
      plt.plot(x_[0], x_[1], '*', marketfacecolor='none', markeredgecolor=c)
    else:
      plt.plot(x_[0], x_[1], c+'o' if y_==0 else c+'+')
  
plt.figure()
vis_data(x_train, y_train, c='r')
plt.show()

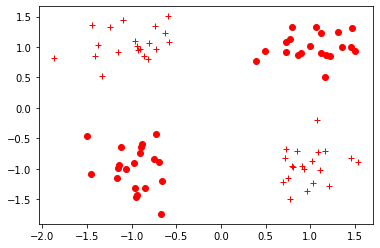
그림 3-1. 코드 결과

데이터가 잘 생성된 것으로 보인다. 이제 넘파이 벡터 형식의 데이터들을 파이토치 텐서로 바꿔주자.

x_train = torch.FloatTensor(x_train)
x_test = torch.FloatTensor(x_test)
y_train = torch.FloatTensor(y_train)
y_test = torch.FloatTensor(y_test)

이제 신경망 모델을 만들자. 파이토치에서 신경망은 신경망 모듈(torch.nn.Module)을 상속받는 파이썬 클래스로 정의한다. nn.Module을 상속받으면 파이토치 프레임워크에 있는 각종 도구를 쉽게 적용할 수 있다.
신경망의 구조와 동작을 정의하는 생성자를 모델 클래스에 먼저 정의한다. NeuralNet클래스의 객체를 만들 때 input_size와 hidden_size를 입력받도록 정의한다. input_size는 신경망에 입력되는 데이터의 차원이다.
다음 입력된 데이터가 인공 신경망 통과하면서 거치는 연산들을 정의한다. torch.nn.Linear()함수는 행렬곱과 편향을 포함한 연산을 지원하는 객체를 반환한다. linear_1과 linear_2객체는 나중에 함수로 쓰일 수 있다. relu()와 sigmoid()는 각 단계에서 수행할 활성화 함수이다.
마지막으로 생성자 __init__()에서 정의한 동작들을 차례대로 실행하는 forward() 함수를 구현한다. linear_1은 입력 데이터에 [input_size, hidden_size] 크기의 가중치를 행렬곱하고 편향을 더하여 [1, hidden_size]꼴의 텐서를 반환한다. 이 텐서에 relu()함수를 적용하여 0보다 작으면 0을, 0보다 크면 입력값을 그대로 출력하도록 한다. 그 다음 다시 linear_2 함수를 거쳐 [1,1] 꼴의 텐서를 반환한다. 이 텐서를 sigmoid() 거쳐 0과 1사이의 확률값으로 변환되도록 한다. 0에 가까우면 클래스 0, 1에 가까우면 클래스 1이 반환될 것이다.

class NeuralNet(torch.nn.Module):
  def __init__(self, input_size, hidden_size):
    super(NeuralNet, self).__init__()

    self.input_size = input_size
    self.hidden_size = hidden_size
    
    self.linear_1 = torch.nn.Linear(self.input_size, self.hidden_size)
    self.relu = torch.nn.ReLU()
    self.linear_2 = torch.nn.Linear(self.hidden_size, 1)
    self.sigmoid = torch.nn.Sigmoid()
  
  def forward(self, input_tensor):
    linear1 = self.linear_1(input_tensor) # __call__ 함수로 구현하면 해당 객체 호출하여 데이터 입력시 출력값 리턴 가능하다!
    relu = self.relu(linear1)
    linear2 = self.linear_2(relu)
    output = self.sigmoid(linear2)
    return output

이제 신경망 객체 생성 후 학습에 필요한 여러 변수와 알고리즘을 정의한다.

model = NeuralNet(2, 5)
learning_rate = 0.03
criterion = torch.nn.BCELoss()
epochs = 2000
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)

criterion은 여러 오차 함수 중 어떤 함수를 쓸 것인지에 대한 변수로, 여기서는 이진 교차 엔트로피인 BCELoss() 함수를 사용한다. 에폭은 전체 학습 데이터를 총 몇 번 모델에 입력할지 결정하는 변수이다. 에폭은 너무 작게 설정하면 모델이 충분히 학습되지 않을 수 있으며, 크게 설정하면 학습이 오래걸린다. 학습에 사용할 최적화 알고리즘은 확률적 경사하강법(SGD)를 선택할 것이다. optimizer는 step() 함수를 부를 때 마다 가중치를 학습률만큼 갱신한다. 그래서 moel.parameter() 함수로 모델 내부의 가중치를 SGD() 함수에 입력하고 학습률도 SGD() 함수에 입력했다.

이제 아직 학습하지 않은 모델의 성능을 보자.

model.eval()
test_loss_before = criterion(model(x_test).squeeze(), y_test)  # 모델의 결과값과 레이블값의 차원을 맞추기 위해 squeeze() 함수 사용
print('Before Training, test loss is {}'.format(test_loss_before.item()))  # 텐서 속 숫자를 스칼라 값으로 변환하기 위해 item() 함수 사용

(결과) Before Training, test loss is 0.645291805267334 # 100번 찍어 64번 틀린다는 뜻

이제 신경망을 학습시켜보자. 모델에 train() 함수를 호출하여 학습 모드로 바꿔준다. 에폭마다 새로운 경사값을 계산할 것이므로, zero_grad() 함수 사용하여 경사값을 0으로 설정한다. 그리고 앞서 생성한 모델에 학습데이터를 입력하여 결과값을 계산한다. 이어 결과값의 차원을 학습 레이블의 차원과 같게 만들고 오차를 계산한다. 100 에폭마다 오차를 출력하여 학습 잘 되는지 확인할 것이다. 마지막으로 오차 함수를 가중치로 미분하여 오차가 최소가 되는 방향을 구하고, 그 방향으로 모델을 학습률만큼 이동시킨다.

for epoch in range(epochs):
  model.train()
  optimizer.zero_grad()
  train_output = model(x_train)
  train_loss = criterion(train_output.squeeze(), y_train)
  if epoch % 100 == 0:
    print('Train loss at {} is {}'.format(epoch, train_loss.item()))
  train_loss.backward()
  optimizer.step()

(결과) Train loss at 0 is 0.7493579983711243
       Train loss at 100 is 0.6670505404472351
       Train loss at 200 is 0.6009105443954468
       Train loss at 300 is 0.5226348042488098
       Train loss at 400 is 0.4344537854194641
       Train loss at 500 is 0.34321680665016174
       Train loss at 600 is 0.2647372782230377
       Train loss at 700 is 0.20638075470924377
       Train loss at 800 is 0.1649305522441864
       Train loss at 900 is 0.13516339659690857
       Train loss at 1000 is 0.11338607966899872
       Train loss at 1100 is 0.09709872305393219
       Train loss at 1200 is 0.08457082509994507
       Train loss at 1300 is 0.07471741735935211
       Train loss at 1400 is 0.06681334227323532
       Train loss at 1500 is 0.060360174626111984
       Train loss at 1600 is 0.05501692369580269
       Train loss at 1700 is 0.0505140945315361
       Train loss at 1800 is 0.046674009412527084
       Train loss at 1900 is 0.04336244985461235

훈련을 시킬수록 오차가 점점 줄어들었다. 신경망 학습이 끝났으니, 이제 학습된 신경망의 성능을 시험해보자. 모델을 평가 모드로 바꾸고 예측값과 정답간 오차를 구한다.

model.eval()
test_loss_before = criterion(torch.squeeze(model(x_test)), y_test)
print('After Training, test loss is {}'.format(test_loss_before.item()))

(결과) After Training, test loss is 0.051639605313539505

학습을 시키니 성능이 훨신 개선되었다!

이제 학습된 모델을 state_dict() 함수 형태로 바꾸고 .pt 파일로 저장하자. state_dict() 함수는 모댈 내 가중치들이 딕셔너리 형태로 표현된 데이터이다.

torch.save(model.state_dict(), './model.pt')
print('state_dict format of the model: {}'.format(model.state_dict()))

(결과) state_dict format of the model: OrderedDict([('linear_1.weight', tensor([[ 1.6538, -1.5809],
       [-0.8564,  0.9028],
       [-1.2493,  1.3215],
       [-0.7172,  0.5184],
       [-1.5437,  1.6288]])), ('linear_1.bias', tensor([-0.3444, -0.0939, -0.2914,  1.8187, -0.3649])), ('linear_2.weight', tensor([[ 2.2818,  0.9448,  1.6297, -1.8723,  2.0588]])), ('linear_2.bias', tensor([-1.0846]))])

만약 이 학습된 모델을 다시 사용하고 싶다면, 다음 코드처럼 이 파일을 읽어들여 새로운 신경망 객체에 해당 모델의 가중치를 바로 적용할 수 있다.

new_model = NeuralNet(2, 5)
new_model.load_state_dict(torch.load('./model.pt'))
new_model.eval()
print('벡터 [-1, 1] 레이블 1을 가질 확률: {}'.format(new_model(torch.FloatTensor([-1, 1])).item()))

(결과) 벡터 [-1, 1] 레이블 1을 가질 확률: 0.9861477613449097